Il fallait que je revienne sur mes pas, que je refasse ce chemin parcouru dont j’avais brisé tous les fils. De ce lieu souterrain, je n’ai rien à dire. Je sais qu’il eut lieu, et que désormais, la trace en est inscrite en moi et dans les textes que j’écris.

Georges Perec, Les lieux d’une ruse

Nos journées ont pour titre La passe comment conclure ? Il y a donc dans ces journées présentes la volonté d’un moment conclusif, d’un acte, mais aussi la reconnaissance de la nécessité d’un deuxième tour puisque ce sont nos deuxièmes journées sur la passe. Je me suis donc livré à la relecture des travaux sur la passe que nous avions présentés il y a moins de deux ans, y compris mon propre texte1.

Cette relecture a été l’occasion de m’interroger de nouveau sur quelques phrases de Lacan trouvées dans le séminaire intitulé justement Le moment de conclure.

Il s’agit de la définition de la fin de l’analyse comme deuxième tour.

” La fin de l’analyse, c’est quand on a deux fois tourné en rond, c’est-à-dire retrouvé ce dont on est prisonnier ; recommencer deux fois le tournage en rond, c’est pas certain que ce soit nécessaire, il suffit qu’on voie ce dont on est captif, et l’inconscient c’est ça. C’est la face de réel (…), c’est la face de réel de ce dont on est empêtré. (…) L’analyse ne consiste pas à ce qu’on soit libéré de ses sinthomes (…). L’analyse consiste à ce qu’on sache pourquoi on en est empêtré (…). De sorte que l’analyse est liée au savoir. “ (10 janvier 1978)

Ces phrases ont été prononcées quelques jours après les Assises de l’École freudienne sur l’expérience de la passe2 où Lacan a parlé, vous le savez, d’échec.

Cette nécessité du deuxième tour est comme je l’avais déjà souligné la fois précédente, une nécessité topologique. Elle résulte de la structure en double boucle du signifiant. Les deux boucles sont distinctes parce que le signifiant qui se répète est différent de lui-même, mais le point où la coupure se recoupe est le point de réel, la rencontre du réel comme ” le même “. On retrouve là l’opposition du signifiant et de la lettre. Cette coupure en double boucle est une constante topologique, lorsqu’elle se réalise sur le tore, elle transforme celui-ci en double bande de Moebius qui après le recollement d’un de ses bords vient enserrer l’objet a en formant un cross-cap. C’est la topologie résumée dans l’Etourdit.

Dans Le Séminaire XI, Lacan montre avec la double boucle sur le cross-cap, comment le désir de l’analyste permet à la demande de traverser le plan de l’identification et opère la séparation du a dans une analyse. Même après l’introduction des noeuds, nous voyons ressurgir avec le noeud borroméen fait de tores cette nécessité d’une double coupure, que ce soit dans L’insu que sait de l’une-bévue s’aile à mourre où il faut une deuxième coupure pour assurer un nouveau retournement du tore symbolique, que ce soit dans le séminaire Le moment de conclure que nous évoquons aujourd’hui où le retournement, dit Lacan, pare aux effets de la coupure, c’est-à-dire que dans un noeud borroméen fait de tores, le retournement du tore du symbolique permet ensuite une coupure transversale sans rupture du noeud, puisqu’il s’agit alors d’une transformation du tore en bande biface.

Si dans l’une des phrases que nous avons citées, Lacan met en doute la nécessité d’un deuxième tour, c’est, pourrait-on avancer, parce que l’analyse est d’emblée un deuxième tour, c’est-à-dire une relecture du savoir inconscient.

Il y a en effet une écriture déposée dans l’inconscient qui constitue la face de réel dont parle Lacan. L’art de l’analyste consiste en une lecture, l’analyste lit ” Autrement ” dans ce que dit l’analysant, en jouant sur l’équivoque et sur la coupure, et sa lecture met en évidence cette autre face, ” la face de réel de ce dont on est empêtré “.

Pour nous détendre, je vais vous lire un petit poème oulipien3 qui va illustrer cette lecture Autre.

” Il faut faire ici bas

Le devoir sans faux-pas

subsister sans folie

est le but de ma vie.

l’amour, toujours l’amour

est d’un faible secours.

La pire absurdité :

chercher la volupté. ”

Peut-être que vos oreilles averties ont déjà entendu ce dont il s’agit. Si vous écrivez les quatre premiers vers sur l’endroit d’une feuille, les quatre derniers sur son envers après l’avoir retournée, non pas transversalement mais de haut en bas. Si ensuite, vous fabriquez avec cette feuille une bande de Moebius, en la recollant après une demi-torsion, il suffit alors de pratiquer une coupure longitudinale au ” milieu ” de cette bande de Moebius, c’est-à-dire entre les deux premiers vers et les suivants pour obtenir le poème que vous lirez sur les deux faces de la bande de Moebius double obtenue.

” Il faut faire ici bas, l’amour, toujours l’amour

Le devoir, sans faux pas, est d’un faible secours.

La pire absurdité : subsister sans folie

chercher la volupté est le but de ma vie. ”

Il faut bien sûr se garder d’exagérer la valeur démonstrative de ce petit poème oulipien, il serait trompeur par exemple d’y voir la métaphore d’une analyse réussie ou de croire que l’inconscient c’est simplement le contraire du conscient, de plus la topologie n’est ici qu’un support, alors que nous avons affaire à une écriture qui est topologique dans sa texture même. Pourtant l’intérêt de ce petit jeu est de nous montrer que le texte latent était bien là dans le texte manifeste sur la face unique de la bande de Moebius et non pas dans de mystérieuses profondeurs, c’est la coupure qui en permet la lecture, qui constitue du même coup l’inconscient comme autre face.

En voici une autre illustration : une analysante rapporte à son analyste le rêve suivant : ” Je suis couchée dans un lit, ou sur le divan, et vous êtes allongé aussi, mais sur un autre lit à l’envers, je vous passe un papier avec un rêve écrit dessus, vous me dites quelque chose que je n’arrive pas à comprendre. ” Ce rêve est exemplaire en ce qu’il réclame dans son texte même sa propre lecture par le sujet supposé savoir, la relation de transfert y est explicite, pourtant cette lecture nécessite une coupure et joue sur l’équivoque puisque le texte latent est ” l’analyste lit à l’envers le rêve “. Comme il est fréquent de le vérifier cliniquement, il est remarquable que dans notre langue le lieu des ébats amoureux et du rêve renvoie à la lettre, ” la psychanalyse, des histoires de lit ! ” a-t-on pu si bien dire involontairement.

L’inconscient, en effet, relève de l’écriture, le rêve, le lapsus, le mot d’esprit se définissant par le lisible, c’est ce que Lacan souligne dans la même leçon du Moment de conclure citée au début.

” Le lisible, c’est en cela que consiste le savoir. ” Il y a de l’écriture dans l’inconscient, et le sujet supposé savoir, c’est le ” sujet supposé savoir lire Autrement “. Que l’écriture touche ainsi au Réel a conduit Lacan à proposer dans cette même leçon une passe par écrit, mais il note aussitôt comme pour modérer l’enthousiasme, que ” ces écrits on ne les lira pas, (…) on en a trop lu ” et il rappelle la proximité bien connue du papier et de l’objet anal.

Dans le ” sujet supposé savoir “, c’est le sujet qui est supposé et non pas le savoir, ce sujet supposé au savoir n’existe pas, cela s’écrit S(A). C’est de cette destitution qu’il est question dans la passe.

La supposition d’un sujet supposé savoir se nourrit d’un ” Savoir absolu ” terme que Lacan reprend de Hegel. ” Das absolute Wissen “, le ” Savoir absolu “, but de l’Histoire selon Hegel, n’est pas qu’un savoir total couché sur le papier, c’est un savoir qui se sait lui-même, il y faut donc un sujet.

S’il y a bien un savoir écrit dans le lieu de l’Autre, dont Lacan nous a donné une idée dans son texte ” Parenthèses des parenthèses “4, ce savoir comporte un manque S(A). L’Autre sait, mais il n’est pas un sujet, et l’analyste opère la séparation entre ce savoir, cette structure, et le sujet supposé savoir.

Nous avons eu cet été l’occasion d’étudier le séminaire D’un Autre à l’autre, ce qui va nous permettre d’éclairer ce que je viens de dire en reprenant la formalisation de Lacan à partir de la théorie des ensembles.

Dans ce séminaire, Lacan assimile la relation d’un signifiant à un autre signifiant à une relation d’appartenance comme dans la théorie des ensembles. Il utilise ainsi le concept de paire ordonnée qui associe deux ensembles distincts a et b, l’ensemble {{a}, {a,b}}, la paire ordonnée met en relation un des ensembles a avec non pas l’autre ensemble b, mais avec la relation du premier au second, cette relation étant elle-même un ensemble. Ce concept de paire ordonnée est propre à formaliser le signifiant. En effet, un signifiant n’est lui-même qu’une différence avec un autre signifiant ; il faut donc considérer la relation qui est la différence comme étant elle-même un signifiant.

Si S Æ A vient noter la relation d’un signifiant à l’Autre, il faut substituer à A ce qu’il est, c’est-à-dire le signifiant de l’ensemble constitué par le rapport de S à A.

S Æ A devient S Æ (S Æ A). Mais A peut de nouveau être remplacé par la relation qu’il subsume. Ce mouvement infini de substitution peut se figurer par des cercles incluant d’autres cercles à l’infini.

Il y a un lien direct entre cette structure répétitive et la répétition que Freud a isolée. L’objet a est dans cette structure précisément ce qui la cause, le cercle le plus interne constitue son index.

L’Autre étant le lieu d’inscription des signifiants, cet Autre doit aussi bien se trouver à l’extérieur de tous les cercles que dans le cercle le plus interne.

Si le cercle le plus interne vient se conjoindre au cercle le plus externe nous retrouvons alors la structure topologique du tore ou de la bouteille de Klein. C’est une structure où l’Autre s’inclut lui-même, figurant ainsi le savoir absolu. (fig. 1)

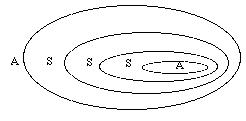
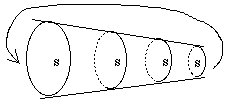
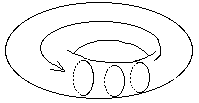
Figure 1

Il y a donc un lien de structure entre la répétition, un objet a insaisissable et le sujet supposé savoir incarnant ce savoir absolu.

C’est à ce point que Lacan dans le séminaire D’un Autre à l’autre fait intervenir le paradoxe de Russel qui vous le savez a conduit les mathématiciens à reformuler l’axiomatique de la théorie des ensembles. L’ensemble de tous les ensembles qui ne se contiennent pas eux-mêmes, se contient-il lui-même ? S’il ne se contient pas lui-même, il est incomplet, s’il se contient lui-même, il ne répond plus à sa propre définition.

Le signifiant répond à cette définition de ne pas se contenir lui-même parce qu’il est précisément différent de lui-même. Mais si tout signifiant représente le sujet pour un autre signifiant, existe-t-il un grand Autre, ensemble des signifiants en tant qu’ils se rapportent à un autre signifiant ?

Ce grand Autre tombe comme nous le voyons sous le coup du paradoxe de Russel, il est inconsistant.

A la fin du séminaire D’un Autre à l’autre Lacan reprend cette construction à partir du trait unaire et de l’ensemble vide. Chaque inscription du trait unaire dans l’Autre vise à la répétition d’une jouissance énigmatique et constitue après coup le premier trait comme représentant le sujet auprès d’un autre signifiant.

La partition d’un ensemble quelconque met en évidence l’ensemble vide, ainsi la partition de l’ensemble dont le trait unaire 1 est le seul élément constitue un ensemble dont les sous ensembles sont 1 et l’ensemble vide Ø. Lacan applique de nouveau l’axiome de la paire ordonnée à ce nouvel ensemble {1 {1, Ø}}. Les deux 1 se distinguent d’une appartenance différente, et il est facile de réitérer l’opération comme précédemment pour le couple { S, A }. Cette formalisation permet à Lacan d’identifier A à l’ensemble vide, cet ensemble vide qui reste le même d’une inscription à l’autre, c’est l’un-en-plus ” l’enforme ” de l’objet a. Mais il est exclu ici que l’ensemble vide se contienne lui-même, donc que l’Autre se contienne lui-même.

Que l’Autre soit un ensemble vide peut se comprendre en reprenant la définition mathématique5 de l’ensemble vide, comme l’ensemble dont les éléments vérifient l’énoncé x _ x, puisqu’il s’agit là de la propriété même des signifiants. Cette mise en place formalise la structure que l’acte analytique doit séparer du ” sujet supposé savoir “.

Il est intéressant de remarquer la proximité de cette construction avec celle des nombres naturels en mathématiques, comme partitions consécutives de l’ensemble vide.

En effet, à partir de Ø cette partition est la suivante

Ø, {Ø}, {Ø {Ø}}, {Ø {Ø {Ø}}}, …

0 1 2 3 …

Dans cette construction l’ensemble vide est la base ; dans la construction de Lacan c’est au contraire un ensemble vide ” en plus “, et l’ensemble des traits unaires constitue un ensemble ” infiniment profond “, où le trou toujours renouvelé est un lieu d’inscription.

Une nouvelle théorie mathématique, celle des hyperensembles6, recoupe exactement les questions que soulevait Lacan dans ce séminaire D’un Autre à l’autre. Cette théorie examine les conséquences de la négation d’un axiome, l’axiome de fondation.

Les axiomes de la théorie des ensembles lui permettent de ne pas être contradictoire, c’est-à-dire inconsistante, ils écartent les paradoxes tels que celui de Russel ou encore celui de l’ensemble de tous les ensembles. Ces axiomes ont pour effet par exemple de réduire la taille des ensembles, toute collection n’est pas un ensemble. Ainsi certaines relations ne peuvent pas définir d’ensemble, x oe x n’est pas collectivisante, mais x = x non plus, alors que x _ x définit bien un ensemble, l’ensemble vide.

L’axiome de fondation dû à Von Neumann a aussi pour fonction de protéger la théorie des paradoxes. Cet axiome énonce que tout ensemble non vide contient un autre ensemble dont l’intersection avec le premier ensemble est vide.

” x [ x _ Ø _ \$ y (y Œ x et y ” x = Ø)]

Tout ensemble contient un sous-ensemble qui n’a aucun élément commun avec lui, c’est le cas de l’ensemble vide lui-même.

Cet axiome interdit les suites infinies descendantes d’ensembles comme

… Œ x n + 1 Œ xn Œ … x2Œ x1 Œ x0

En effet, il est impossible dans x0 d’isoler un sous-ensemble qui ne contienne pas lui-même un autre sous-ensemble appartenant à x0. L’axiome de fondation exclut les cycles tel que

x1 Œ x2 Œ x3 … Œ xn +1 Œ xn Œx1

En effet, dans l’ensemble { x1… xn}, tout sous-ensemble a des éléments communs avec x1.

En particulier, x Œ x est de ce fait interdit, un ensemble ne peut s’inclure lui-même.

L’axiome de fondation montre le lien entre ces trois structures qu’il rejette : les chaînes descendantes à l’infini, les cycles, l’inclusion d’un ensemble dans lui-même. Ce sont précisément ces trois structures que Lacan rencontre dans son séminaire D’un Autre à l’autre.

En fait, l’axiome de fondation n’est pas indispensable à la théorie classique des ensembles de Zermelo-Fraenkel, ainsi il est démontré que si cette théorie est sans contradiction sans cet axiome, alors elle l’est aussi avec.

L’axiome de fondation ne donne pas non plus une définition du concept d’ensemble fixe et définitive puisque le théorème d’incomplétude de Gödel démontre que toute propriété formulable dans le cadre de la théorie qui inclut cet axiome n’est pas de façon certaine vraie ou fausse.

C’est ainsi que P. Aczel a récemment proposé une théorie des hyperensembles, avec un axiome d’antifondation, où on admet l’existence d’ensembles qui appartiennent à eux-mêmes. Par exemple, il existe un hyperensemble _ = {_}, il existe également un hyperensemble X à deux éléments : l’ensemble vide et lui-même, et un hyperensemble infiniment profond : {0 {1 {2 {3 {4… }}}}}.

Il est démontré que si la théorie classique des ensembles ne conduit à aucune contradiction, alors il en est de même pour la théorie des hyperensembles.

Il est remarquable que Lacan dans ce séminaire D’un Autre à l’autre lorsqu’il s’interrogeait justement sur la relation du sujet au grand Autre à l’aide de la théorie des ensembles, ait construit de tels hyperensembles. Les ensembles {S {S {S, A}}} ou {1 {1 {1, 0}}} sont des hyperensembles infiniment profonds ou constituent des cycles lorsque A s’inclut lui-même, la figure topologique du tore est d’ailleurs explicitement utilisée par les auteurs traitant des hyperensembles. (fig. 2)

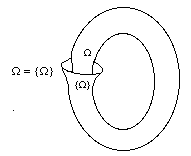
Figure 2

Comme nous venons de le montrer, il existe un lien entre les suites infinies descendantes d’ensembles, les cycles et l’inclusion d’un ensemble dans lui-même, trois structures que Lacan rencontre dans son séminaire, ce sont les structures que l’axiome de fondation rejette. Celui-ci stipule qu’une chaîne descendante rencontre un terme conclusif qui peut être l’ensemble vide.

C’est peut-être ce que la névrose obsessionnelle illustre, le bien nommé axiome de fondation se trouve annulé, d’où la problématique paternelle de l’obsessionnel et son rejet de l’impératif phallique, la chaîne signifiante ne peut trouver sa consistance que dans ses propres éléments ou dans leur enchaînement rigoureux puisqu’elle est privée d’une référence au réel.

La ” descente à l’infini ” qui résulte de cette annulation de l’axiome de fondation expliquerait pourquoi chez l’obsessionnel toute faille, fente, entre-deux, coupure, représentant l’ensemble vide qui surgit comme Réel, est source de ratiocinations, de vérifications sans fin. Bien entendu, cette coupure à la fois fascinante et douloureuse ne cesse de se manifester avec violence et dans le discours même de l’obsessionnel, ainsi cette idée parasite et obsédante de ” langue coupée ” dont l’un d’eux me parlait.

Dans la névrose, répétition et savoir absolu s’entretiennent l’un l’autre selon une structure torique. La conclusion de la cure équivaut alors à une coupure du tore, dans une même opération l’objet est découpé et le sujet supposé au savoir destitué.

Pratiquée sur le tore symbolique du noeud borroméen, cette coupure peut se concevoir comme seconde par rapport au retournement et donc conserver au noeud sa structure borroméenne.

La structure reste borroméenne, ce que l’analyse a modifié c’est la place du sujet par rapport au savoir, puisque le tore a été démasqué comme tore, sa structure a été retournée et ouverte. Ce n’est pas la même chose de se déplacer dans une surface torique en en subissant les effets, que de se promener avec une carte, cette carte n’est rien d’autre que celle du signifiant. Malheureusement elle ne peut être fournie au sujet avant le voyage, et ce voyage se fait de nuit, par temps d’orage avec des éclairs de temps en temps pour illuminer le paysage.

C’est ainsi que l’on peut comprendre la phrase de Lacan citée en début sur le fait que l’analyse ne consiste pas à se libérer de ses ” sinthomes ” mais à savoir pourquoi on en est empêtré. Cela ne veut pas dire que l’analyse ne guérisse pas, mais la guérison ne s’obtient pas en supprimant directement le symptôme, le désir de l’analyste ne se confond pas avec le désir de guérir.

C’est précisément sur ces questions que Lacan revient dans la même année que le séminaire Le moment de conclure, à la fin du congrès sur La transmission7.

En évoquant la passe et la transmission de la psychanalyse, Lacan en vient à dire que ” la psychanalyse est intransmissible… C’est bien ennuyeux que chaque psychanalyste soit forcé – puisqu’il faut bien qu’il y soit forcé – de réinventer la psychanalyse “.

Pourtant Lacan dit attendre toujours de la passe quelque chose qui concerne justement la guérison : ” Alors comment se fait-il que, par l’opération du signifiant, il y ait des gens qui guérissent ? […] Malgré tout ce que j’en ai dit à l’occasion, je n’en sais rien. C’est une question de truquage. Comment est-ce qu’on susurre au sujet qui vous vient en analyse quelque chose qui a pour effet de le guérir, c’est là une question d’expérience dans laquelle joue un rôle ce que j’ai appelé le sujet supposé savoir. Un sujet supposé savoir, c’est un redoublement. Le sujet supposé savoir, c’est quelqu’un qui sait. Il sait le truc […] la façon dont on guérit une névrose. […] J’aimerais bien savoir, par quelqu’un qui témoignerait dans la passe qu’un sujet – puisque c’est d’un sujet qu’il s’agit – est capable de faire plus que ce que j’appellerai le bavardage ordinaire. […] Si l’analyste ne fait que bavarder, on peut être assuré qu’il rate son coup, le coup qui est d’effectivement lever le résultat, c’est-à-dire ce qu’on appelle le symptôme. “

 Ces propos peuvent surprendre, n’est-il pas contradictoire de dire que l’analyse ne consiste pas à se libérer des ” sinthomes ” et d’évoquer ici la guérison, de pointer la destitution du sujet supposé savoir et d’en parler ici comme de quelqu’un qui sait ” le truc ” qui lève le symptôme ?

En fait si l’analyste opère la séparation entre a et l’idéal du moi ainsi que la coupure entre la structure et le sujet supposé savoir, il le fait dans la mesure où c’est le désir de l’analyste qui l’anime, c’est cela ” le truc “, un désir énigmatique que la passe devrait éclairer.