Jeu, savoir et connaissance

Jean BRINI

Je voudrais essayer de m’appuyer sur certaines choses qui ont été dites hier et ce matin, notamment à propos de cette remarque de Lacan, dans le séminaire « Problèmes Cruciaux », où il observe que dans le triangle moebien qu’il nous a proposé, entre Sujet, Sexe et Savoir, un terme, le Sexe, serait absent dans le jeu. Je souhaiterais en effet vous proposer, en m’appuyant sur la théorie des jeux, une illustration des conséquences de ce fonctionnement limité à deux seulement des trois pôles, le Sujet et le Savoir. Nous savons bien sûr, à quoi nous allons aboutir : nous observerons les conséquences de l’hypothèse d’un savoir clos, auquel rien ne saurait ex-sister.

Un premier abord de cette question concerne l’apologue des trois prisonniers, cette histoire que Lacan appelait son petit sophisme personnel. En effet, il me semble que jamais Lacan n’a appliqué le terme de jeu à cet apologue. Pourtant, il s’agit d’un problème qui a été largement étudié par la théorie des jeux, et que celle-ci a réussi à formaliser rigoureusement. Il m’a semblé intéressant d’examiner de plus près cette formalisation, pour illustrer quel est le prix à payer pour la mettre en œuvre.

L’énoncé du problème, tel que la théorie des jeux le reformule, est le suivant : le directeur de la prison est en quelque sorte un meneur de jeu qui énonce une règle : vous pouvez chacun avoir sur le dos soit un rond blanc, soit un rond noir. Dans une heure, vous me remettrez une enveloppe, dans laquelle vous aurez glissé une feuille, sur laquelle vous aurez écrit votre opinion sur la situation : soit « je sais », soit « je ne sais pas ». Je lirai alors publiquement le contenu de vos réponses. Si aucune réponse n’est « je sais », le jeu continue l’heure suivante, et ainsi de suite jusqu’à ce que l’une au moins des enveloppes contienne la réponse : « je sais ».

Le déroulement du jeu est ainsi scandé non plus par son mécanisme propre, comme dans l’apologue lacanien, mais par la règle. A ce prix-là, on peut donner une description totalement logicisée de ce qui s’y passe. Cette description est donnée par la figure suivante :

L’état initial donne la liste de tous les cas possibles. Le meneur du jeu annonce alors que la configuration « trois ronds noirs » n’est pas possible, donnant ainsi le départ du jeu. Il rend en effet le déroulement du jeu possible, en rendant « publique » l’information : « l’un au moins d’entre vous porte un rond blanc » ou, ce qui est équivalent : « à voir deux noirs, on sait qu’on est un blanc ». Le paradoxe est que cette information, tous les joueurs la possèdent déjà, puisque chacun a devant lui deux ronds blancs. L’important est que cette information est désormais publique, et reconnue par chacun comme telle. C’est pour rendre compte de ce paradoxe que la théorie des jeux a introduit le terme de « common knowledge », pour désigner ce partenaire « en plus », dont le savoir importe autant dans le déroulement du jeu que celui des agents. La suite du déroulement est alors automatique : au bout d’une heure, chaque prisonnier, voyant deux blancs, annonce : « je ne sais pas ». Il devient alors « common knowledge » que les trois configurations comportant deux noirs et un blanc ne sont pas réalisées. L’heure suivante, si l’un des prisonniers voyait un noir, il se saurait donc nécessairement blanc. Comme ce n’est pas le cas, chacune annonce à nouveau « je ne sais pas ». A cet instant, tous savent qu ‘ils portent un rond blanc, et l’annoncent une heure plus tard.

Ainsi, toute la mise en forme logique du jeu consiste dans ce découpage du progrès logique en publications successives d’énoncés dès lors ramenés à de simples informations. Alors qu’avons-nous perdu dans cette logicisation ? Bien évidemment la hâte, c’est à dire ce qui fait précisément le cœur de l’apologue lacanien, et du coup, également la nécessité d’une assertion de certitude anticipée. Le jeu formalisé, bien réglé, n’exige plus aucune anticipation de la part des sujets qui y prennent part.

La question devient alors de préciser quelle est la nature de cette distorsion si importante à nos yeux, introduite par la formalisation. Pour cela, je voudrais tenter de vous présenter quelques éléments de la théorie formalisée de la connaissance qui sous-tend cette description du jeu des trois prisonniers. Ces éléments sont tirés d’un article de Robert Aumann (Epistémologie interactive), où celui-ci donne un exposé unifié des formalisations de la connaissance utilisées en théorie des jeux.

Le premier de ces éléments aboutit à la notion de common knowledge, notion déjà explorée par J.M. Lasry en 1984 (Ornicar N° 30), et qui désigne ce qui est public, ce qui a « été dit entre » les agents du jeu. Le point de départ réside dans la donnée d’un opérateur de connaissance K défini par une axiomatique très semblable à celle des probabilités :

L’axiome 1 s’écrit :

Il peut se lire : «si l’agent i connaît E, alors, E est vrai ». Pour poser cet axiome, il y a un préalable posé au départ qui est le « tout ». Celui-ci représente l’ensemble des états du monde, et qui correspond à l’ensemble des possibles des probabilités. Dans le cas de l’apologue des trois prisonniers, par exemple, l’ensemble des états du monde est l’ensemble des 8 états décrits dans la figure. Dans d’autres cas plus complexes, les états seront plus nombreux. Dans ce « tout », un ensemble E sera spécifié comme l’ensemble des états du monde pour lesquels une certaine proposition sera vraie. Pour le complémentaire de E, la proposition sera fausse.

K _iE Ì E est en soi une assertion qui peut susciter l’étonnement. Elle énonce en effet qu’on ne connaît que des choses vraies. De fait, la théorie épistémique résout cette difficulté en distinguant connaissance et croyance, cette dernière étant définie comme une connaissance assortie d’une probabilité.

L’axiome 2 peut également paraître surprenant. Il s’agit de l’axiome dit d’introspection. Il s’écrit :

Il peut se lire : « si l’agent i connaît E, alors l’agent i sait qu’il connaît E », et signifie aussi bien qu’il n’y a pas de savoir insu.

Les autres axiomes de la théorie ne nous occuperont pas ici.

Il est intéressant d’observer que ces axiomes sont très exactement ce que réfute Lacan dans un passage du séminaire « Les non-dupes errent » où il dit « La logique épistémique part de ceci que le savoir, c’est forcément savoir le vrai (axiome n° 1). Vous ne pouvez pas savoir où ça mène, dit-il, à des folies, ne serait-ce que celle-ci, enfin, en faux duquel s’inscrit le savoir inconscient, qu’il est impossible de savoir quoi que ce soit, supposé vrai comme tel, sans le savoir (axiome n°2). D’où il résulte qu’il est tout à fait impossible, ce n’est pas très difficile à obtenir enfin il y a un mathématicien très sympathique qui se rompt à Hintikka et qui en a fait la très jolie démonstration, on m’en a communiqué les notes, que le savoir qui se supporterait de ce qu’on ne sache pas qu’on sait est strictement inconsistant, enfin impossible à énoncer dans la logique épistémique… ouais. »

Je dois dire que je n’ai pas réussi à retrouver cette démonstration. Néanmoins, on peut noter que la logique épistémique nous permet une écriture de l’hypothèse du savoir insu. Ce pourrait être :

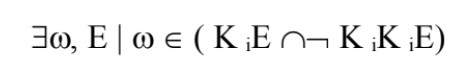
qui peut se lire : il existe au moins un état du monde w et un événement E tels qu’en w, l’agent i connaît E sans savoir qu’il connaît E.

Cette lecture n’est d’ailleurs possible que du fait que le terme anglais « knowledge » se traduit aussi bien par « savoir » que par « connaissance ».

Dans la suite, Lacan nous fait remarquer que Freud s’était très rapidement inquiété des rapports entre le savoir inconscient et la vérité, en s’apercevant qu’un rêve pouvait parfaitement s’avérer mensonger. Nous sommes à nouveau en contradiction avec l’axiome 1 : Si je sais E, alors E est vrai.

Je voudrais maintenant vous proposer, en rapprochant deux textes, une illustration de ce que Lacan désigne par « les folies » où nous mène la logique épistémique. Le premier texte est extrait d’un article de deux élèves d’Aumann, qui s’interrogent sur la cardinalité de l’espace des états, en d’autres termes sur la «taille » de l’ensemble des possibles :

La question est : combien y a-t-il d’états de connaissance concernant un fait donné lorsque plusieurs agents sont impliqués. Cette question a une influence sur le problème de la nomination des états de connaissance. S’il n’y a qu’un nombre fini ou dénombrable d’états, alors ceux-ci peuvent avoir des noms finis, dans un langage ayant un alphabet fini ou dénombrable, mais si la cardinalité de l’ensemble de ces états est celle du continu, alors il est impossible de les nommer tous, tout à fait de la même façon que nous ne pouvons nommer tous les points de notre espace physique. Dans un tel cas, l’idée que les agents connaissent le modèle épistémique qui décrit leur propre connaissance doit être interprété avec beaucoup de précautions. Si le modèle est suffisamment riche, alors, connaître, dans ce contexte, ne signifie pas que les agents peuvent parler en langage ordinaire de tous les états ».

Voilà donc où nous mène le déploiement technique de la logique épistémique : l’article démontre qu’effectivement, l’espace des états est continu, et qu’il est par conséquent impossible de nommer tous ses éléments. Conclusion qui pourrait aussi passer pour un cas particulier de démonstration de l’impossibilité d’un métalangage. De la nécessité de cette découverte, il est également rendu compte par la remarque de C.Melman (Intervention aux journées sur le séminaire « Problèmes Cruciaux ») où il disait : « L’obsessionnel, de quoi est-il malade ? Il n’accepte pas que ça commence au zéro. Il ne veut pas du zéro. Il forclot le zéro, et donc, pour lui, tout commence au « un ». Mais à partir du moment où ça commence au un, il n’y a plus aucune césure dans la suite des nombre, et non seulement il n’y a plus aucune césure, mais encore, il va se passer entre eux cet événement épouvantable qui s’appelle la puissance du continu ». C’est exactement ce que nous rapportent ces auteurs. «Sans cesse entre deux nombre je peux en tirer un autre, et puis un autre, et puis encore un autre, et finalement tout ca se tient, tout ça se touche, et c’est évidemment le sacrilège suprême et l’horreur ».

Voilà donc l’une de ces « folies » dont Lacan nous prévenait qu’elles pouvaient résulter de la logique épistémique. Et nous voyons maintenant quelle en est l’origine : il s’agit du refus du zéro.

Qu’est-ce à dire ? Comment pourrions-nous expliciter en quoi consiste ce refus ? Il me semble que nous pouvons repérer ce refus du zéro dans certains choix qui ont été opérés dès le XIXe siècle, au moment de la fondation de la logique formalisée, le fameux « calculus ratiocinator » que Leibniz appelait de ses vœux et dont la théorie des jeux est l’héritière légitime. On trouve en effet au fondement de cette logique la notion d’ « Univers du Discours », notion à laquelle Lacan consacre plusieurs leçons de son séminaire « Logique du fantasme », pour la réfuter. Le terme d’Univers du Discours a été introduit pour la première fois par De Morgan, contemporain de Boole. A cette époque Lewis Carroll écrivait : « La copule, vielle actrice toujours un peu susceptible demande : est-ce moi qui prendrai le ne-pas, ou dois-je le laisser au prédicat ? » et De Morgan répond sans ambiguïté que c’est au prédicat qu’il revient de prendre la négation. Il affirme en effet : « La logique découvre ainsi que tout terme a toujours dans la pensée un négatif, même s’il n’existe pas de nom qui lui corresponde dans le discours ordinaire, et qu’un nom, en général, quel qu’il soit, divise les êtres entre ceux qui ont les qualités qu’il dénote et ceux qui en sont dépourvus. Par conséquent positif et négatif deviennent totalement relatifs, un terme quelconque étant toujours négatif relativement à son contraire. » Ainsi pour De Morgan, il est légitime de considérer comme équivalentes les deux propositions « nul x n’est y » et « tout x est non-y ». Le zéro considéré comme nombre de l’ensemble vide, est donc ici radicalement évacué de la logique, dans la mesure ou « nul x » est positivé. Il me semble qu’on peut considérer, en suivant C.Melman, ce point comme l’origine des conclusions auxquelles arrive la théorie des jeux.

On peut remarquer, et j’en resterai à cette observation que, comme J.L.Chassaing le faisait remarquer hier, Freud souligne, dans sa Psychopathologie de la vie quotidienne, le caractère innombrable des significations que peut prendre un terme. Il me semble que ce qui est en jeu dans la puissance du continu que démontre la théorie des jeux est du même ordre.