Nous savons l’importance des relations entre la psychanalyse et le jeu, aussi bien le game que le play. Cet intérêt (1) se retrouve évoqué par Lacan dès le séminaire II, avec le jeu de pair-impair, aussi bien qu’avec le texte d’Edgar Poe consacré à la lettre volée.

Dans une conférence faite en juin 1955, intitulée  » Psychanalyse et Cybernétique, ou de la nature du langage « , Lacan évoque par ailleurs d’emblée en relation avec cet intérêt, le travail de Pascal.

 » C’est bien parce que l’on s’est posé la question que, corrélativement à la naissance des sciences exactes, a commencé de naître ce calcul qu’on a plutôt mal que bien compris – calcul des probabilités, lequel apparaît pour la première fois sous une forme véritablement scientifique en 1654 avec le traité de Pascal sur le triangle arithmétique, et se présente comme le calcul, non pas du hasard, mais des chances, de la rencontre en elle-même.

Ce que Pascal élabore dans cette première machine qu’est le triangle arithmétique se recommande de l’attention du monde savant en ceci, qu’il permet de trouver immédiatement ce qu’un joueur a le droit d’espérer à un certain moment où on interrompt la succession des coups qui constitue une partie. Une succession de coups est la forme la plus simple qu’on puisse donner à l’idée de la rencontre. Tant qu’on n’est pas arrivé au terme de la suite des coups prévue par la convention, quelque chose est évaluable, à savoir les possibilités de la rencontre comme telle. Il s’agit de la place, et de ce qui y vient ou qui n’y vient pas, de quelque chose donc qui est strictement équivalent à sa propre existence. A la science de ce qui se retrouve à la même place, se substitue ainsi la science de la combinaison des places en tant que telles. Cela, dans un registre ordonné qui suppose assurément la notion de coup, c’est-à-dire celle de scansion.

Tout ce qui, jusque-là, avait été science des nombres devient science combinatoire. Le cheminement plus ou moins confus, accidentel, dans le monde des symboles, s’ordonne autour de la corrélation de l’absence et de la présence. Et la recherche des lois des présences et absences va tendre à cette instauration de l’ordre binaire qui aboutit à ce que nous appelons cybernétique. « 

Et effectivement, Pascal rédige en 1654 le Traité du triangle arithmétique2, celui-ci ne sera publié qu’en 1665. Par ailleurs, le 29 juillet 1654, Pascal adresse à Fermat une lettre3 dans laquelle il rend compte de la règle des partis. C’est à partir de ces textes que l’on accorde à Pascal le mérite d’avoir fondé le calcul des probabilités.

En très bref, le problème des partis peut s’énoncer ainsi : deux joueurs décidant d’arrêter une partie avant son achèvement, il s’agit de déterminer comment l’enjeu restant doit être réparti entre eux. Chaque joueur prendra d’abord la somme minimale qui lui reviendrait quoi qu’il advienne. Quant à la somme restante, elle sera partagée par moitié s’il y a  » autant de hasard que l’un des joueurs gagne que l’autre « , si la partie est continuée. Ainsi Pascal détermine une manière de faire – certaine – en face de l’incertitude. Aussi pouvait-il déclarer dans Les Pensées que  » l’on travaille pour l’incertain sur mer en bataille « , mais qu’avant lui  » on n’a pas vu la règle des partis qui démontre qu’on le doit « .

Nous pouvons donc entrevoir d’emblée la différence de position d’avec Descartes. Pour Pascal, pas de preuves de l’existence de Dieu mais, face à l’incertitude de l’existence divine, une possibilité de trouver une position certaine : manière spécifique à l’auteur des Pensées de soutenir la déchirure qu’il éprouve entre Science et Foi.4

Lacan reviendra ensuite sur le Pari de Pascal en 1966, à sa séance du 2 février lors du séminaire l’Objet de la psychanalyse. Et d’emblée, il indique ce qu’il amène de neuf à la lecture que l’on peut faire et que l’on a faite habituellement du pari :

 » Il semble que nulle part, personne ne s’est avancé dans ce texte du pari de ce point de vue, que ce n’est pas un « on » qu’il s’agit de convaincre, que ce pari est le pari de Pascal lui-même, d’un je, d’un sujet qui nous révèle sa structure. « 

Dans cette séance, Lacan citera longuement le Pari de Pascal, le texte même du Pari, soit Infini, rien.5 Texte qui, selon d’aucuns, n’aurait été retrouvé qu’après le décès de son auteur, sous forme de deux feuillets griffonnés dans les poches du défunt. Par l’argument du Pari, Pascal s’efforce de démontrer – pour ainsi dire mathématiquement – que dans l’ignorance, l’homme a tout intérêt à parier pour l’existence de Dieu et plus précisément pour la religion chrétienne.

 » Examinons donc ce point, et disons :  » Dieu est, ou il n’est pas. » Mais de quel côté pencherons-nous ? La raison n’y peut rien déterminer : il y a un chaos infini qui nous sépare. Il se joue un jeu, à l’extrémité de cette distance infinie, où il arrivera croix ou pile. Que gagnerez-vous ? Par raison, vous ne pouvez faire ni l’un ni l’autre ; par raison, vous ne pouvez défendre nul des deux.

Ne blâmez donc pas de fausseté ceux qui ont pris un choix ; car vous n’en savez rien.

– Non ; mais je les blâmerai d’avoir fait, non ce choix, mais un choix ; car, encore que celui qui prend croix et l’autre soient en pareille faute, ils sont tous deux en faute : le juste est de ne point parier.

– Oui ; mais il faut parier ; cela n’est pas volontaire, vous êtes embarqué. Lequel prendrez-vous donc ? Voyons. Puisqu’il faut choisir, voyons ce qui vous intéresse le moins…

– Votre raison n’est pas plus blessée, en choisissant l’un que l’autre, puisqu’il faut nécessairement choisir. Voilà un point vidé. Mais votre béatitude ? Pesons le gain et la perte, en prenant croix que Dieu est. Estimons ces deux cas : si vous gagnez, vous gagnez tout ; si vous perdez, vous ne perdez rien. Gagez donc qu’il est, sans hésiter.

– Cela est admirable. Oui, il faut gager ; mais je gage peut-être trop.

– Voyons. Puisqu’il y a pareil hasard de gain et de perte, si vous n’aviez qu’à gagner deux vies pour une, vous pourriez encore gager ; mais s’il y en avait trois à gagner, il faudrait jouer (puisque vous êtes dans la nécessité de jouer), et vous seriez imprudent, lorsque vous êtes forcé à jouer, de ne pas hasarder votre vie pour en gagner trois à un jeu où il y a pareil hasard de perte et de gain. Mais il y a une éternité de vie et de bonheur.

Mais il y a ici une infinité de vie infiniment heureuse à gagner, un hasard de gain contre un nombre fini de hasards de perte, et ce que vous jouez est fini. Cela ôte tout parti : partout où est l’infini, et où il n’y a pas infinité de hasards de perte contre celui de gain, il n’y a point à balancer, il faut tout donner. Et ainsi, quand on est forcé à jouer, il faut renoncer à la raison pour garder la vie, plutôt que de la hasarder pour le gain infini aussi prêt à arriver que la perte du néant… « 

Dans son séminaire  » D‘un Autre à l’autre « , Lacan va formaliser ce pari sous forme d’un petit carré divisé en quatre parties dans lequel les deux carrés du dessus rendent compte de ce qui se passerait si le parieur rencontre l’existence de Dieu, les deux carrés du dessous si le parieur rencontre la non-existence de Dieu. Les carrés de gauche reprenant ce que devient ce qui se mise alors que les carrés de droite reprennent ce qui éventuellement se gagne. Et Lacan d’indiquer :  » Voici donc comment les choses se figurent, et si j’ai fait cette matrice, c’est non pas qu’elle me paraisse suffisante, mais qu’elle soit l’ordinaire, à quoi l’on se tienne. « 6

Il pourrait à première vue paraître étonnant que dans les cases du dessus, c’est-à-dire lorsqu’il est parié pour l’existence de Dieu, la mise devienne un zéro ; en fait, cette mise devient zéro parce que s’il gagne, le sujet ayant affaire à une infinité de vies heureuses, cette infinité comprend d’office la mise de la vie du sujet. Et c’est ceci qui est expliqué par Lacan lorsqu’il dit

 » L’infini dont il s’agit, celui que Pascal illustre, a figure d’un signe analogue à celui qui est là, l’infini des nombres entiers, car, c’est seulement par rapport à lui que devient inefficient l’élément de départ, je veux dire neutre, que c’est à ce titre qu’il en devient zéro, puisqu’il s’identifie à l’addition du zéro à l’infini, le résultat de l’addition ne pouvant se figurer que du signe qui désigne un des deux termes. « 7

Nous pouvons ensuite lire la partie inférieure de cette matrice : il est parié, mais ce sera la non-existence de Dieu. Dans ce cas la mise est le petit a et ce qui est gagné, c’est évidemment zéro. En fait, tout est perdu. Ce qui permet de mettre un signe = entre le carrré supérieur de gauche et celui inférieur de gauche étant donné qu’il y a équivalence entre le zéro de la mise de celui qui parie et qui rencontre l’existence de Dieu et les petits carrés du bas où il s’agit de parier et de rencontrer sa non-existence. Démonstration de ce que Pascal nous soutient, à savoir qu’il vaut mieux parier : il y a tout à gagner à parier pour l’existence de Dieu.  » Si vous gagnez, vous gagnez tout, si vous perdez, vous perdez rien. « 

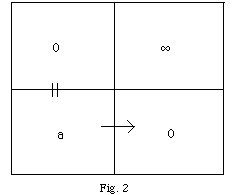
Mais nous pouvons appréhender la confusion introduite dans ce Pari : c’est que parier et rencontrer l’existence de Dieu est assimilé à  » parier pour « , et parier et rencontrer la non-existence de Dieu est considéré comme  » parier contre « , sous le prétexte que de toutes façons, nous sommes  » embarqués « . Or ceci est en fait un abus, car précisément ce qui est gommé dans cette disposition, c’est l’intervention du sujet, en l’occurrence de Pascal lui-même.  » Il n’y a pas que le partenaire, il y a l’enjeu « , rappelle Lacan.

Lacan veillera donc à spécifier ce qu’il faut introduire pour rendre correctement compte du Pari. Et il va ramasser les deux carrés du dessus en un seul carré qu’il va inscrire à gauche au-dessus et les deux carrés du bas en un seul carré à droite ; en distinguant par ailleurs celui qui, dans le Pari,  » parie pour  » et celui qui au contraire  » parie contre « . Nous obtenons ensuite ceci :

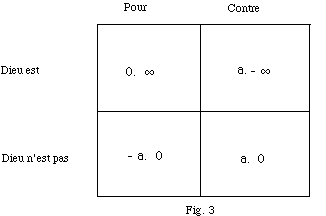
Que l’on peut expliciter comme suit :

– le carré supérieur gauche : il s’agit de celui qui  » parie pour  » l’existence de Dieu et qui la rencontre effectivement, donc qui est gagnant ; ce qu’il mise, c’est petit a, il obtient l’infini, des vies heureuses ; mais l’infini comprenant d’office celle qu’il a engagée, sa mise est réduite à zéro. D’où  » 0. + ƒ  » ;

– le carré supérieur droit : c’est celui qui  » parie contre  » l’existence de Dieu mais qui néanmoins rencontre effectivement l’existence de Dieu ; lui effectivement mise le petit a, sa vie, mais il perd son pari, et il obtient l’enfer, donc moins l’infini, moins l’infini des vies heureuses. D’où  » a. – ƒ  » ;

– le carré inférieur droit : le sujet  » parie contre  » l’existence de Dieu alors que celui-ci n’existe pas ; il ne joue donc pas, il ne se met pas à la table du jeu ; il ne lâche pas ce qu’il a ! il garde donc petit a, et étant donné qu’il n’y a pas d’existence de Dieu, il n’obtient pas l’infinité des vies heureuses, donc, il n’obtient rien, il obtient zéro en réponse. D’où  » a. 0  » ;

– le carré inférieur gauche : là, le sujet  » parie pour  » l’existence de Dieu, mais Dieu n’existe pas ; il est entièrement perdant, il obtient zéro mais il est le perdant du pari et ce qu’il a engagé est marqué d’un signe négatif, moins a. D’où  » – a. 0 « . Ce sera celui que Lacan appellera le  » pépère « , celui qui consent à lâcher l’objet pour rien.

Ceci amènera Lacan à faire se redéployer les nouveaux carrés qu’il a introduits – selon un système qui sera d’ailleurs analogue à ce qu’il fera dans le schéma de la sexuation8 – ; il remet les nouvelles notations dans un carré à quatre éléments : dans le carré supérieur gauche, petit a ; moins petit a dans le carré inférieur gauche ; moins l’infini dans le carré supérieur droit ; zéro dans le carré inférieur droit. Soit que l’on y retrouve déployé ce qui était  » oublié  » dans la matrice induite par la formulation de Pascal.

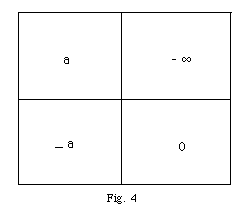
Ce que Lacan nous montre dès lors dans ce Pari de Pascal, c’est comment ce dernier  » essayait de nous flouer « . En effet, l’auteur des Pensées nous floue sur la perte.

 » Dans la religion chrétienne, le croyant paraît échanger un objet égal à 0 avec une jouissance infinie promise dans l’Autre. Mais la renonciation dont il s’agit est, à double titre une forfaiture : il renonce pour jouir infiniment de l’Autre et c’est à l’aune de cette jouissance infinie qu’il engage son existence ; un Autre de l’Autre la garantit. En réalité il sait que cela ne lui coûte rien et qu’il ne renonce pas à l’objet comme s’il feignait de perdre a pour mieux jouir de l’Autre par l’intermédiaire de a. « 9

Une autre manière de le dire, c’est que Pascal nous floue sur la dimension de l’acte en jeu dans le Pari : il nous préconise un pari, et en ce sens il valorise l’acte, mais de le déduire d’une combinatoire – dont d’ailleurs il gomme le sujet – il en élude la dimension spécifique d’acte, soit la perte que celui-ci inclut.

Pascal fait porter l’acte sur la croyance en Dieu, celle-ci n’étant pas démontrable, mais il se récupère en démontrant par  » la règle des parties  » que le gain que peut amener le pari de croire est infini par rapport à la perte ; ce faisant il fait porter l’incertitude à assumer, sur l’existence de Dieu, et masque ainsi que l’incertitude à assumer est celle du parieur, de sa mise, soit du  » je  » qui s’engage.

Voilà pourquoi sans doute D.R. Dufour fait du Pari de Pascal une  » merveille de la pensée binaire. «  10

Jean-Pierre Lebrun

1 – cf. à ce sujet : M. Darmon,  » Remarques sur la psychanalyse et le jeu « , in Essais sur la topologie lacanienne , p. 88 et suivantes.

2 – Pascal B., Œuvres complètes, Flammarion, 1963, pp. 50-63.

3 – Pascal B., ibid, pp. 43-49.

4 – Voir à ce propos Minois G., L’Église et la science, histoire d’un malentendu, 2 volumes, Paris, Fayard, 1990, pp. 64-67.

5 – Pascal B., ibid., pp. 550-552.

6 – Lacan J., D’un Autre à l’autre, séance du 29 janvier 1969, inédit. Il est exact que c’est ce modèle qui formalise ce type de jeu : cf. à ce propos Gardner M., Théorie des jeux, carte cachée et terriers, Math’ Festival, Bibliothèque pour la science, éd. Pour la Science, SARL, 1981, pp. 23-31.

7 – Lacan J., ibid p. 141.

8 – Soit qu’à partir des impasses du carré d’Aristote, Lacan extrait les formules droites du schéma.

9 – Cathelineau P.C.,  » Du Trou « , in Le Discours psychanalytique n° 19, juin 1986, p. 27.

10 – Dufour D.-R., Les mystères de la trinité, Gallimard 1990, p. 460.